Jak możemy przeczytać w artykule Brenta Yorgeya opublikowanym w magazynie The Monad.Reader, „funktor to najbardziej podstawowa i wszechobecna klasa w Haskellu„. [1] Często okazuje się jednak, że zrozumienie koncepcji funktorów i związanych z nimi zawiłości nie jest takie proste dla osób, wkraczających w świat programowania funkcyjnego. O ile elementy języka, które zazwyczaj poznaje się wcześniej – typy, listy czy funkcje (i to nawet uwzględniając zagadnienia związane z curryingiem oraz częściową aplikacją) – jawią się jeszcze jako dosyć zrozumiałe, to królestwo funktorów (również tych aplikatywnych), monoidów oraz monad przysparza na ogół znacznie więcej problemów.

Spróbujemy zatem na spokojnie przyjrzeć się owym groźnym bytom i oswoić je. Zaczniemy oczywiście od funktorów, ale na razie pominiemy aspekty matematyczne związane z tym pojęciem. Chociaż z pewnością warto je zrozumieć, to bynajmniej nie są one niezbędne do sprawnego programowania w Haskellu.

Co to są funktory?

Bardzo często można spotkać się z wyjaśnieniem funktorów na przykładzie pudełek. Wewnątrz owych pudełek przechowujemy jakieś wartości, a funktory opisują jak można te wartości przekształcać zwykłymi funkcjami, aby finalnie otrzymać nowe wartości, ale wciąż zapakowane w swoje pudełka. Jeśli lubicie tego typu porównania, polecam artykuł Functors, Applicatives, And Monads In Pictures, który pełen jest ilustacji takich jak ta poniżej.

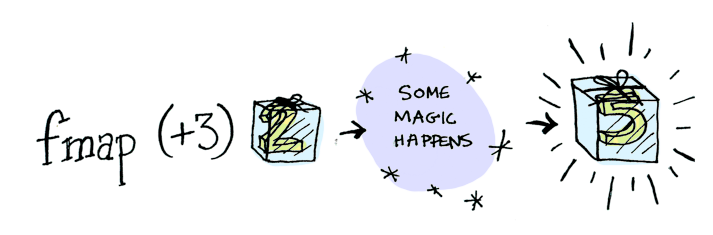
Mamy zatem wartości, które opakowane są w pewien kontekst. Takim kontekstem może być na przykład lista, krotka, wektor, albo haskellowe typy Either oraz Maybe. Zapewne prędzej lub później będziemy chcieli wywoływać funkcje, które operują na przechowywanych wewnątrz tych kontenerów wartościach. Jak to zrobić?

Należy wykorzystać klasę typów Functor (więcej o klasach typów przeczytasz w tym wpisie). Deklaruje ona metodę – fmap o następującej sygnaturze:

fmap jest poniekąd uogólnieniem, być może znanej Ci dobrze, funkcji map, która operuje tylko na listach. Przyjmuje ona dwa argumenty:

• funkcję, która bierze argument pewnego typu (a) i zwraca wartość o takim samym lub innym typie (b).
• funktor (f) sparametryzowany typem a

Rezultatem działania jest również funktor, ale sparametryzowany typem b. Prowadzi nas to do wniosku, że funktor jest po prostu kontenerem, który można mapować.

Przykłady

Jednym z prostszych funktorów, znakomicie wpasowującym się w koncepcję „pudełka przechowującego dane”, jest typ Maybe. Może on zawierać jakąś wartość (używamy wtedy konstruktora Just a) albo i nie (od tego mamy konstruktor Nothing). Gdy wartość, na jakiej chcemy operować, nie jest nigdzie spakowana, zaaplikowanie do niej funkcji jest trywialne:

Kiedy jednak nasza wartość znajduje się wewnątrz kontenera, taki sposób nie zadziała. W celu wypakowania jej, zaaplikowania funkcji, a następnie ponownego zapakowania możemy oczywiście dokonywać akrobacji pokroju:

Ale czy nie łatwiej wykorzystać charakterystyczną dla funktorów funkcję fmap?

Jak już wspomniałem, przykłady innych obecnych w Haskellu funktorów, to chociażby Either oraz lista – co ciekawe, dla tego ostatniego typu, fmap jest zdefiniowane w następujący sposób:

A przecież mapowanie list to już całkiem zrozumiała sprawa, prawda? 😉

Tajemnicze operatory

Z funktorami wiążą się dwa enigmatyczne operatory: <$> oraz <$. Pierwszy z nich zdefiniowany jest w bibliotece Control.Applicative i jest po prostu infiksowym synonimem dla funkcji fmap. Pozwala on więc nieco uprościć nasze wyrażenia, np.:

Łatwo zapamiętać z uwagi na podobieństwo do operatora $, którego moglibyśmy użyć (choć tutaj akurat nic on nie zmienia) gdyby w wyrażeniu powyżej pozbyć się kontenera:

Drugi z funktorowych operatorów – <$ – jest metodą typeclassy Functor, ale prawdopodobnie na ogół nie będziemy potrzebowali implementować go po swojemu (można robić to np. w celu poprawy wydajności [2]). Przyjrzyjmy się więc domyślnej definicji:

Mamy zatem złożenie dwóch funkcji – fmap oraz const, co w praktyce sprowadza się do zastąpienia przechowywanej w kontenerze wartości na tą, która podana jest jako pierwszy argument:

Bifunktory

Istotnym ograniczeniem dla funktorów, o którym należy pamiętać, jest rodzaj konstruktora typu, jakiego wolno tu użyć. Mianowicie, instancjami klasy funktor mogą być wyłącznie typy z jednym parametrem. Nie z zerem, nie z dwoma lub z trzema, ale z dokładnie jednym.

Jak zatem radzić sobie, kiedy nasz typ ewidentnie nie pasuje jako kandydat do zostania fuktorem, a bardzo chcemy go nim uczynić? W przypadku braku parametrów – potrzebujemy większej generalizacji. Kiedy zaś konstruktor typu używa więcej niż jednego parametru – rozwiązań jest kilka.

Dla przykładu, typ Either a b jest sparametryzowany dwoma typami. A jednak jest funktorem. Jak? Można to osiągnąć przy pomocy częściowej aplikacji:

Rezultat działania Either jako funktora jest taki, że tylko wartości prawidłowe (utworzone konstruktorem Right) są mapowane, natomiast te, które zazwyczaj oznaczają stan błędu (kontruktor Left), nie są w żaden sposób przekształcane:

Co jednak jeśli interesuje nas mapowanie obu typów – zarówno prawego, jak i lewego? Z pomocą na szczęście przybywa klasa Bifunctor, która zamiast metody fmap definiuje bimap:

Przekazujemy do niej dwie funkcje, a każda z nich może operować na innych typach (oczywiście odpowiednio do typów parametrów naszego funktora). Co ciekawe, Either jest nie tylko instancją funktora, ale też bifunktora. W takim kontekście prezentuje się następująco:

Pamiętajmy tylko, że bifunktory należy wcześniej zaimportować z modułu Data.Bifunctor.

Warto jeszcze wspomnieć, że jedno z popularniejszych użyć bifunktora to operacje na dwuelementowych krotkach:

Szersze spojrzenie

Na sam koniec parę słów o tym, jak można nieco szerzej spojrzeć na funktory w świecie Haskella, wykraczając poza słynne pudełka (a wręcz wyskakując z nich). Gdyby zerknąć do znajdującej się w Wikipedii definicji, dowiemy się, iż „funktor to odwzorowanie jednej kategorii do drugiej„.

Jeśli zastanawiasz się w jaki sposób ma się to do naszej dwuargumentowej funkcji fmap, to tajemnica powinna wyjaśnić się, jeśli sygnaturę tej funkcji zapiszemy nieco inaczej niż wcześniej (o tym, że można tak zrobić pisałem tutaj, chociaż akurat na przykładzie innego języka funkcyjnego – OCamla):

Gdyby zaś abstrahować od samej klasy typów o nazwie Functor, to przykładem idealnie wpisującego się w tę definicję funktora jest również funkcja length, zwracająca długość listy, bowiem robi ona dokładnie to co napisaliśmy – dokonuje odwzorowania kategorii:

Konkretniej zaś, odwzorowuje kategorię konkatenacji list na kategorię dodawania liczb całkowitych. Więcej na ten temat (włącznie z szerszym omówieniem przytoczonego tu przykładu) można znaleźć w artykule The functor design pattern autorstwa Gabriela Gonzaleza.

Skoro już jesteśmy przy funkcjach, to pora na jeszcze jedną ciekawostkę – w Haskellu funkcje też są funktorami (instancjami klasy Functor). Oznacza to, że można na nich używać funkcji fmap, która jest w tym przypadku zdefiniowana po prostu jako złożenie funkcji (czyli to co wykonujemy przy pomocy operatora .).

Podsumowanie

Jak widać, funktory, mimo groźnie brzmiącej nazwy, nie są wcale tak straszne. Potrafią być za to niezwykle pomocne – możemy w łatwy sposób mapować różne skonteneryzowane dane, unikając przy tym pętli, a także używać tych samych funkcji niezależnie od kontekstu obliczeniowego w jakim znajdują się przetwarzane wartości.

Linki i źródła

1. The Typeclassopedia, B. Yorgey.
2. StackOverflow: What is the purpose of (<$) in the Functor class?
3. Functors Done Quick!
4. Functortown: Functor and Bifunctor.
5. Functors are Containers, B. Milewski.
6. The Functor typeclass.
7. Dokumentacja klasy Functor.